|
4-1 一個點電荷Q與無窮大導體平面相距為d ,如果把它移動到無窮遠處,需要作多少功?
4-2 一個點電荷放在直角導體內部(如圖1所示),求出所有鏡像電荷的位置和大小。
4-3 證明: 一個點電荷q和一個帶有電荷Q的半徑為R的導體球之間的作用力為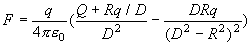
其中D是q到球心的距離(D>R).
4-4 兩個點電荷+Q和-Q位于一個半徑為a的接地導體球的直徑的延長線上,分別距離球心D和-D
。
(1)證明:鏡像電荷構成一電偶集中,位于球心,偶極矩為2a3Q/D2 。
(2)令Q和D分別趨于無窮,同時保持Q/D2不變,計算球外的電場。
4-5 接地無限大導體平板上有一個半徑為a的半球形突起,在點(0,0,d)處有一個點電荷q(如圖2所示),求導體上方的電位。
4-6 求截面為矩形的無限長區域(0<x<a,0<y<b)的電位,其四壁的電位為
j(x,0)=j(x,b)=0 ;
j(0,y)=0 ;
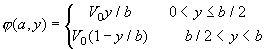
4-7 一個截面如圖3所示的長槽,向y方向無限延伸。兩側的電位是零,槽內。底部的電位為:
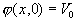 求槽內的電位? 求槽內的電位?
4-8 若上題的底部的電位為: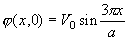
重新求槽內的電位?
4-9 一個矩形導體槽由兩部分構成,如圖4 所示,兩個導體板的電位分別是 V0和零,求槽內的電位。
4-10 將一個半徑為a的無限長導體管平分成兩半,兩部分之間互相絕緣,上半(0<f<p)接電壓V0,下半(p<f<2p)電位為零。求管內的電位。
4-11 半徑為的無窮長圓柱面上,有密度為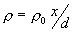 的面電荷,求圓柱面內、外的電位。 的面電荷,求圓柱面內、外的電位。
4-12 將一個半徑為a的導體球置于均勻電場E0中,求球外的電位、電場。
4-13 將半徑為a、介電常數為e的無限長介質圓柱放置于均勻電場E0中,設E0沿x方向,柱的軸沿z軸,柱外為空氣。求任意點的電位、電場。
4-14 在均勻電場中,放置一個半徑為a的介質球,若電場的方向沿z軸,求介質球內外的電位、電場(介質求球的介電常數為e,球外為空氣)。
4-15 已知球面(r=a)上的電位為j=V0cosq,求球外的電位。
4-16 求無限長矩形區域0<x<a,0<y<b第一類邊值問題的格林函數(即矩形槽的四周電位為零,槽內有一與槽平行的單位線源,求槽內電位,如圖5
)。
4-17 推導無限長圓柱區域內(半徑為a)第一類邊值問題的格林函數。
4-18 兩個無限大導體平板間距離為d,其間有體密度 的電荷,極板的電位如圖6
所示,用格林函數法求極板之間的電位。
4-19 分析復變函數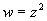 能夠表示的靜電場。 能夠表示的靜電場。
4-20 分析復變函數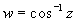 能夠表示那些情形的靜電場。 能夠表示那些情形的靜電場。
4-21 用有限差分法求圖6所示區域中各個節點的電位。
|