3-2 球形電容器內外電極的半徑分別為a、b，其間媒質的電導率為s ，當外加電壓為V0時，計算功率損耗并求電阻。

3-3 一個半徑為a的導體球作為電極深埋地下，土壤的電導率為s ，略去地面的影響，求電極的接地電阻。

3-4 在無界非均勻導電媒質（電導率和介電常數均是坐標的函數）中，若有恒定電流存在，證明媒質中的自由電荷密度為

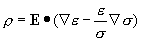
3-5 平板電容器間由兩種媒質完全填充，厚度分別為d1和d2 ，介電常數分別為e 1和e2 ，電導率分別為s1 和s2 ，當外加電壓V0 時，求分界面上的自由電荷面密度。

3-6 內外導體半徑分別為a、c的同軸線，其間填充兩種漏電媒質，電導率分別為s1(a<r<b)和s2(b<r<c)，求單位長度的電阻。

3-7 一個半徑為10厘米的半球形接地導體電極，電極平面與地面重合，如圖1所示，若土壤的電導率為0.01S/m,當電極通過電流為100A時，求土壤損耗的功率。

3-8 一個正n邊形線圈中通過的電流為I,邊長為a,試證此線圈中心的磁感應強度為:

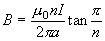
3-9 求載流為I，半徑為a的圓形導線中心的磁感應強度。

3-10 一個載流I1的長直導線和一個載流I2的圓環（半徑為a）在同一平面內, 圓心與導線的
距離是d。證明兩電流之間的相互作用力為 。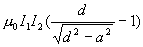

3-11 內、外半徑分別為a、b的無限長空心圓柱中均勻分布著軸向電流I，求柱內外的磁感強度。

3-12 兩個半徑都為a的圓柱體，軸間距為d，d<2a(如圖2所示)。除兩柱重疊部分R外，柱間有大小相等、方向相反的電流，密度為J，求區域R的B。

3-13 證明矢位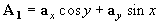 和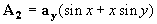 給出相同的磁場B，并證明它們得自相同的電流分布。它們是否均滿足矢量泊松方程？為什么？

3-14 半徑為a的長圓柱面上有密度為Js0的面電流，電流方向分別為：(1)沿圓周方向；(2)沿軸線方向。分別求兩種情形下柱內、外的B。

3-15 一對無限長平行導線，相距2a，線上載有大小相等、方向相反的電流I，求磁矢位A，并求B(如圖3所示)。

3-16 由無限長載流直導線的B求矢位A(用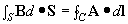 ,并取r=r0處為矢位的參考零點)。并驗證?′A=B。

3-17 證明xy平面上半徑為a ，圓心在原點的圓電流環(電流為I)在z軸上的標位為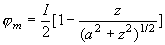

3-18 一個長為L，半徑為a的圓柱狀磁介質沿軸向方向均勻磁化(磁化強度為M0)，求它的磁矩。若L=10cm,a=2cm,M0=2A/m,求出磁矩的值。

3-19 球心在原點，半徑為a的磁化介質球中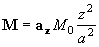，(M0為常數) ，求磁化電流的體密度和面密度。

3-20 證明磁介質內部的磁化電流是傳導電流的(mr-1)倍。

3-21 已知內、外半徑分別為a、b的無限長鐵質圓柱殼(磁導率為m)，沿軸向有恒定的傳導電流I，求磁感強度和磁化電流。

3-22 設x<0的半空間充滿磁導率為m的均勻磁介質，x>0的空間為真空。線電流I沿z 軸方向，求磁感強度。

3-23 已知在半徑為a的無限長圓柱導體內有恒定電流I沿軸向方向。設導體的磁導率為m1，其外充滿磁導率為m2的均勻磁介質。求導體內、外的磁場強度、磁感強度、磁化電流分布。

3-24 試證長直導線和其共面的正三角形 之間的互感為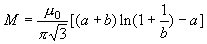

其中a是三角形的高，b是三角形平行于長直導線的邊至直導線的距離(且該邊距離直導線最近)。

3-25 無限長的直導線附近有一矩形回路(二者不共面,如圖3所示),試證它們之間的互感為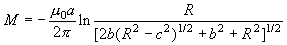

3-26 空氣絕緣的同軸線，內導體的半徑為a，外導體的內半徑為b ，通過的電流為I ，設外導體殼的厚度很薄，因而其儲存的能量可以忽略不計。計算同軸線單位長度的儲能，并由此求到位長度的自感。

3-27 一個長直導線和一個圓環（半徑為a）在同一平面內, 圓心與導線的距離是d，證明它們之間互感為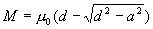

3-28 如圖5所示的長密繞螺線管(單位長度n匝),通過的電流為I ，鐵心的磁導率為m，面積為S，求作用在它上面的力。